Tonal harmony based on major and minor keys is usually called functional harmony. The most important functions of the chords are subdominant, dominant, and tonic (S, D, T). They are usually represented by scale degrees II/IV, V, and I, but other degrees can be substituted for them as well. Tonal harmony without these main functions is called modal harmony.

Why is the subdominant a fourth degree in classical music and a second degree in jazz?

On the surface, this sometimes confusing difference seems like a matter of taste, but there is solid background for it. Theory teaching in classical music traditionally builds on triad harmony; the cadence IV - V - I is a prototype of the S-D-T phenomenon. Jazz and popular music, however, are based on harmonies with four-note chords; there the corresponding cadence S-D-T is in the form II-V-I. What is essential here is the tonic included in the subdominant chord which moves to the leading note and back. Therefore, in triad harmony, the second degree, lacking this decisive note, is not suitable for a basic subdominant. In harmonies with four-note chords, either degree would do, but the second degree with a stronger tonic movement is more common (see above).

Subdominants (IV and IIm7) in harmonies with three- and four-note chords

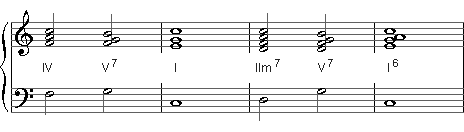
The development of the independent status of the second degree four-note chord is an interesting phenomenon in both classical music and jazz. In 19^th century romantic music, the more and more general subdominant four-note chord was called a sixth (IV6 or L6), also in the general inversion with the second degree note in the bass. The same course is evident in jazz history; Dizzy Gillespie and Thelonius Monk called the minor scale second-degree chord a fourth-degree minor six with the six in the bass (for example, Fm6/D) instead of today's half-diminished chord (Dm7^b5).

Alternative dominants

The following example shows how the minor seventh and its three substitute chords resolve into a tonic triad. The fifth-degree dominant and its tritone substitution Vs (s = substitution) can be considered equally strong as, in both chords, the tritone tension between the dominant chord third and seventh resolves chromatically on both sides. In the relative (Vr) bVII and VII dominant chords, the tritone resolves chromatically only on one side, which makes the resolution weaker. Of these two, bVII is stronger, since it displays the most characteristic resolution for a dominant chord, resolution of a seventh downwards. The corresponding phenomenon in classical music is deceptive resolution V-VI (in a major key) or V-bVI (in a minor key).

Strong root movements

The classification of strength above can be applied to all intervals. All movements in the example are either fourths or seconds. They are usually considered stronger than thirds, which are classified as weak. The following table describes root movement. The first category is the strongest: